Chapter 13 Predicting Gift Size
Among various predictive problems, predicting the next customer spend or donor gift amount is a difficult one. Although we can use—and we do—transaction history, predicting a precise amount with high confidence for every customer or donor is impossible. Even techniques as established as calculating customer lifetime value (CLV) are inaccurate. As Malthouse and Blattberg (2010) concluded, of the top 20% of customers, approximately 55% will be misclassified as not big spenders (that is, false negatives). That’s a big and important population to miss. Using external and internal data can improve the results, as seen in the study of predicting the wallet size of IBM’s customers by Perlich et al. (2007).
A simple, naive model can take the average of all previous transactions and predict that as the next transaction amount, which likely will be close to the actual gift amount. But this model will fail at predicting larger gift sizes, which are typically less than 1% of all transactions. The insurance industry faces the exact same challenge. For example, the majority of car drivers will not get into an accident and an even smaller minority will have high claim amounts (Y. Yang, Qian, and Zou 2017), yet the auto insurance industry must offer reasonable premium rates to remain competitive. The auto insurance industry has had some luck predicting claim size using Tweedie distribution (Tweedie 1984; Jørgensen and Paes De Souza 1994). We can guess so because they remain profitable.
Let’s try all of these approaches.
13.1 Simple Forecasting
Before our analysis gets too complicated, let’s use the simplest approach we can (that is, predicting the next gift size by calculating the average of previous transactions). Let’s use the sample donor data file.
library(readr)
library(dplyr)
donor_data <- read_csv("data/DonorSampleDataCleaned.csv")We will use the previous giving columns to calculate the average. We need to clean up the dollar signs from those columns.
donor_data <- donor_data %>%
mutate_at(.vars = vars(starts_with("PrevFY"), "CurrFYGiving"),
.funs = funs(as.numeric(gsub(x = .,
pattern = "[\\$,]",
replacement = ""))))Now, let’s simply calculate the average of the previous giving columns.
donor_data$CurrFYGiving_pred_sa <- select(
donor_data,
starts_with("PrevFY")) %>%
rowMeans(na.rm = TRUE)How does this prediction stack against the actual giving? Let’s plot and see.
library(ggplot2)
library(scales)
ggplot(donor_data, aes(x = CurrFYGiving,
y = CurrFYGiving_pred_sa)) +
geom_point() +
scale_x_sqrt(labels = dollar) +
scale_y_sqrt(labels = dollar) +
theme_bw() +
geom_smooth()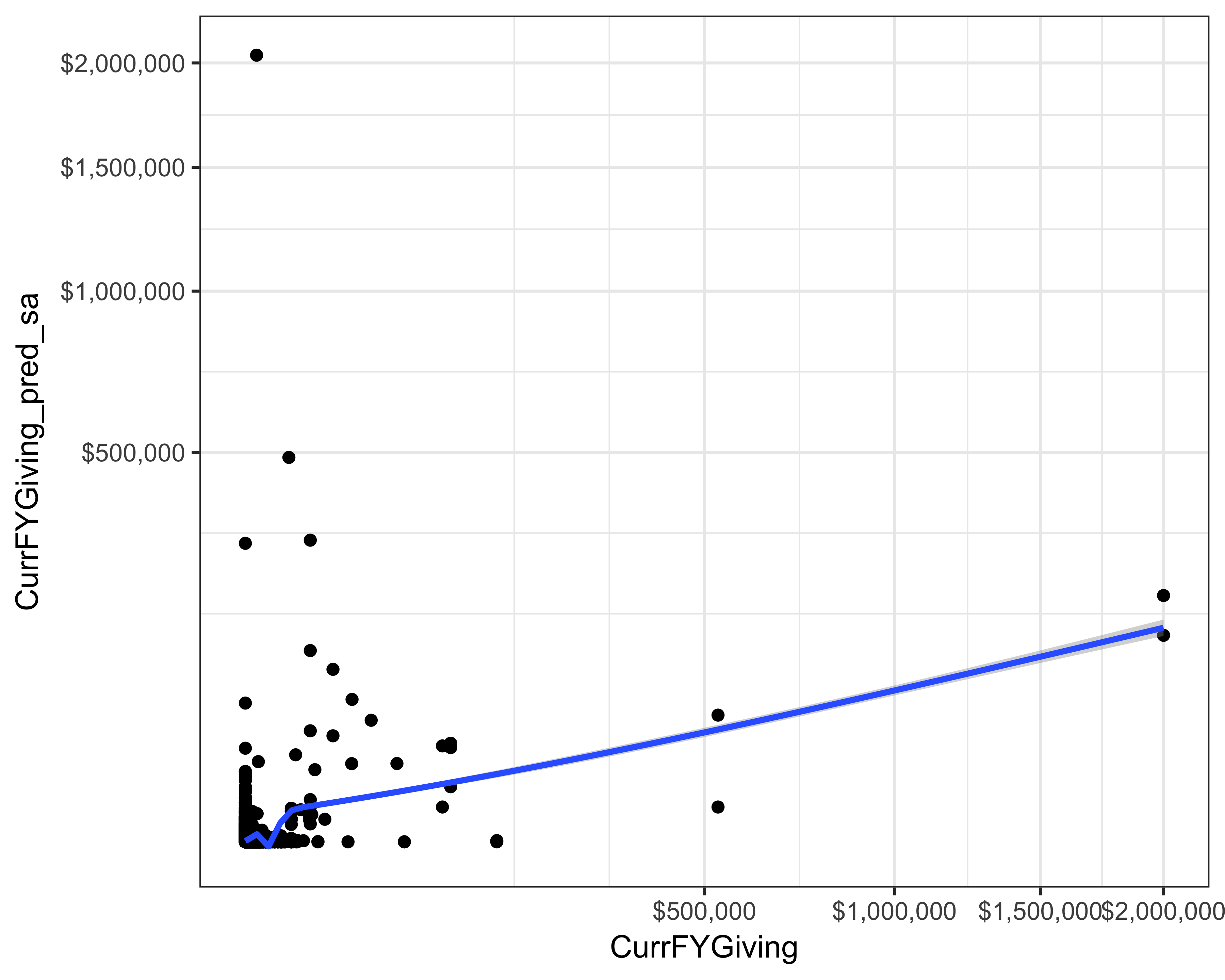
FIGURE 13.1: Actual versus prediction of current FY giving using simple average
You can see in Figure 13.1 that our simple average model either overestimated (when there was no giving) or underestimated (when there was some giving). There are a few predictions that look somewhat accurate—we can say so because we can see some points on an imagined line that goes at 45o. If all the predictions were accurate, all the points would fall on that line. One overall but imperfect measure of accuracy is the Root Mean Square Error (RMSE). We calculate this value by taking the average of the squared difference between the predictions and the actuals. For this calculation, the formula looks like this:
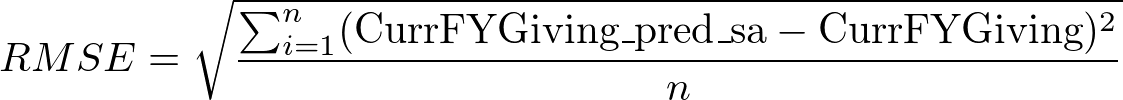
In R code, the calculation is like the following:
rmse_sa <- summarize(
donor_data,
rmse = sqrt(mean((CurrFYGiving_pred_sa - CurrFYGiving)^2)))
rmse_sa$rmse
#> [1] 18555Although such an overall statistic hides the gross mispredictions, it allows us to compare various models with each other. The RMSE for this model is 18,555.
13.2 Quantile Regression
Perlich et al. (2007) used quantile regression to predict the wallet share of IBM’s customers. Since linear regression tries to minimize the mean of the prediction error, it is not helpful when only a few transactions have big values. Therefore, if we can minimize a high quantile error (such as the 90th percentile) we may get good results. Quantile regression extends linear regression by allowing us to minimize the median error or any other quantiles (Koenker 2005). We will use the quantreg package (Koenker 2017).
Before we use this technique, we need to decide the quantile at which the model will estimate (or predict) the giving. Let’s find out the various quantiles.
quantile(donor_data$CurrFYGiving)
#> 0% 25% 50% 75% 100%
#> 0e+00 0e+00 0e+00 0e+00 2e+06Even the 75th percentile is zero. So, we need to determine the quantiles between 90 and 100 then.
quantile(donor_data$CurrFYGiving,
probs = seq(from = 0.9, to = 1, by = 0.01))
#> 90% 91% 92% 93% 94% 95%
#> 0 0 0 0 0 1
#> 96% 97% 98% 99% 100%
#> 25 70 110 244 2000000Let’s use the 98th percentile as the quantile to predict giving.
library(quantreg)
quant_reg1 <- rq(CurrFYGiving ~ PrevFYGiving + PrevFY1Giving +
PrevFY2Giving + PrevFY3Giving +
PrevFY4Giving,
data = donor_data, tau = 0.98)
summary(quant_reg1)
#> Warning in summary.rq(quant_reg1): 155 non-
#> positive fis
#>
#> Call: rq(formula = CurrFYGiving ~ PrevFYGiving + PrevFY1Giving + PrevFY2Giving +
#> PrevFY3Giving + PrevFY4Giving, tau = 0.98, data = donor_data)
#>
#> tau: [1] 0.98
#>
#> Coefficients:
#> Value Std. Error t value
#> (Intercept) 100.00000 128.80697 0.77636
#> PrevFYGiving 0.26531 3.39666 0.07811
#> PrevFY1Giving -0.00441 0.69318 -0.00636
#> PrevFY2Giving 9.34365 8.48873 1.10071
#> PrevFY3Giving 0.02039 0.36324 0.05614
#> PrevFY4Giving 0.01360 0.09012 0.15094
#> Pr(>|t|)
#> (Intercept) 0.43754
#> PrevFYGiving 0.93774
#> PrevFY1Giving 0.99493
#> PrevFY2Giving 0.27103
#> PrevFY3Giving 0.95523
#> PrevFY4Giving 0.88002Next, let’s store the predictions.
donor_data$CurrFYGiving_pred_qr <- predict(quant_reg1)How does this prediction stack against the actual giving? Let’s plot and see.
ggplot(donor_data, aes(x = CurrFYGiving,
y = CurrFYGiving_pred_qr)) +
geom_point() +
scale_x_sqrt(labels = dollar) +
scale_y_sqrt(labels = dollar) +
theme_bw() +
geom_smooth()
#> Warning in self$trans$transform(x): NaNs produced
#> Warning: Transformation introduced infinite values
#> in continuous y-axis
#> Warning in self$trans$transform(x): NaNs produced
#> Warning: Transformation introduced infinite values
#> in continuous y-axis
#> Warning: Removed 1 rows containing non-finite values
#> (stat_smooth).
#> Warning: Removed 1 rows containing missing values
#> (geom_point).
FIGURE 13.2: Actual versus prediction of current FY giving using quantile regression
We can see from Figure 13.2 that quantile regression is overestimating giving. This is understandable because a model that minimizes error at the 98th percentile will over-estimate. And although the regression line seen in the plot shows that this might be a good fit, the RMSE for this model was 30,253.
We can try to improve the results by adding other variables to the model.
quant_reg2 <- rq(CurrFYGiving ~ PrevFYGiving + PrevFY1Giving +
PrevFY2Giving + PrevFY3Giving +
PrevFY4Giving +
AGE + GENDER +
EMAIL_PRESENT_IND,
data = donor_data, tau = 0.98)We run into a problem, however, because of missing values. The predictions would simply omit all the missing values, or we can obtain a missing value as a prediction; both of these results are unhelpful. We can impute these missing values by taking averages or modes of the other existing values in that column, but I’ll leave that exercise for you.
AGE, GENDER, and EMAIL_PRESENT_IND.
13.3 Gradient Tree
Y. Yang, Qian, and Zou (2017) described the gradient tree boosted models using Tweedie distribution for setting the auto insurance premiums. We will use the TDboost package to create this model (Y. Yang, Qian, and Zou 2016). This is a complicated model with many factors at play. Explaining all the details that are happening inside the model is out of the scope of this book.
Let’s go over the minimum parameters we need to use to build this model.
- Number of folds (
cv.folds): We tell the model to divide the data innfolds for training and testing. If we had 10 folds, the model would create 10 different data sets by using 9/10th portion for training and 1/10th for testing. This is a standard approach for training models known as cross-validation and is used to avoid overfitting. - Number of trees (
n.trees): The total number of trees to grow. This parameter controls the boosting which is a method of using results from multiple models and combining them to create a superior model.
Let’s build the model.
library(TDboost)
td1 <- TDboost(CurrFYGiving ~ PrevFYGiving +
PrevFY1Giving + PrevFY2Giving +
PrevFY3Giving + PrevFY4Giving,
data = donor_data, cv.folds = 3, n.trees = 100)
#> CV: 1
#> Iter TrainDeviance ValidDeviance StepSize Improve
#> 1 51.3634 66.5068 0.0010 0.1045
#> 2 51.3418 66.4888 0.0010 0.0001
#> 3 51.2551 66.3733 0.0010 0.0272
#> 4 51.1646 66.2574 0.0010 0.0579
#> 5 51.0787 66.1447 0.0010 0.0488
#> 6 50.9961 66.0383 0.0010 0.0401
#> 7 50.9112 65.9293 0.0010 0.0169
#> 8 50.8290 65.8209 0.0010 0.0525
#> 9 50.7475 65.7161 0.0010 0.0467
#> 10 50.7282 65.7034 0.0010 0.0095
#> 100 45.5861 59.3736 0.0010 0.0138
#>
#> CV: 2
#> Iter TrainDeviance ValidDeviance StepSize Improve
#> 1 55.1576 58.2102 0.0010 0.0470
#> 2 55.1262 58.2050 0.0010 0.0064
#> 3 55.0961 58.1995 0.0010 0.0055
#> 4 55.0106 58.0867 0.0010 0.0412
#> 5 54.9309 57.9800 0.0010 0.0396
#> 6 54.8539 57.8696 0.0010 0.0163
#> 7 54.7850 57.7780 0.0010 0.0909
#> 8 54.7665 57.7765 0.0010 -0.0038
#> 9 54.6933 57.6781 0.0010 0.0175
#> 10 54.6125 57.5697 0.0010 0.0210
#> 100 49.9403 52.1301 0.0010 0.0135
#>
#> CV: 3
#> Iter TrainDeviance ValidDeviance StepSize Improve
#> 1 61.5220 46.1652 0.0010 0.0175
#> 2 61.4101 46.1041 0.0010 0.0215
#> 3 61.3945 46.0609 0.0010 -0.0146
#> 4 61.2936 46.0091 0.0010 0.0159
#> 5 61.1935 45.9602 0.0010 0.0151
#> 6 61.1018 45.9120 0.0010 0.0903
#> 7 61.0108 45.8646 0.0010 0.0919
#> 8 60.9069 45.8031 0.0010 0.0978
#> 9 60.8033 45.7421 0.0010 0.0971
#> 10 60.7356 45.6988 0.0010 0.1073
#> 100 54.5947 41.8167 0.0010 0.0153
#>
#> Iter TrainDeviance ValidDeviance StepSize Improve
#> 1 56.1713 nan 0.0010 0.0748
#> 2 56.0834 nan 0.0010 0.0891
#> 3 55.9879 nan 0.0010 0.0355
#> 4 55.9078 nan 0.0010 0.0719
#> 5 55.8175 nan 0.0010 0.0358
#> 6 55.7961 nan 0.0010 0.0117
#> 7 55.7144 nan 0.0010 0.0851
#> 8 55.6280 nan 0.0010 0.0923
#> 9 55.5509 nan 0.0010 0.0849
#> 10 55.4682 nan 0.0010 0.0716
#> 100 49.5031 nan 0.0010 0.0595
summary(td1, n.trees = 100)
#> var rel.inf
#> 1 PrevFY2Giving 61.63
#> 2 PrevFYGiving 37.00
#> 3 PrevFY4Giving 1.37
#> 4 PrevFY1Giving 0.00
#> 5 PrevFY3Giving 0.00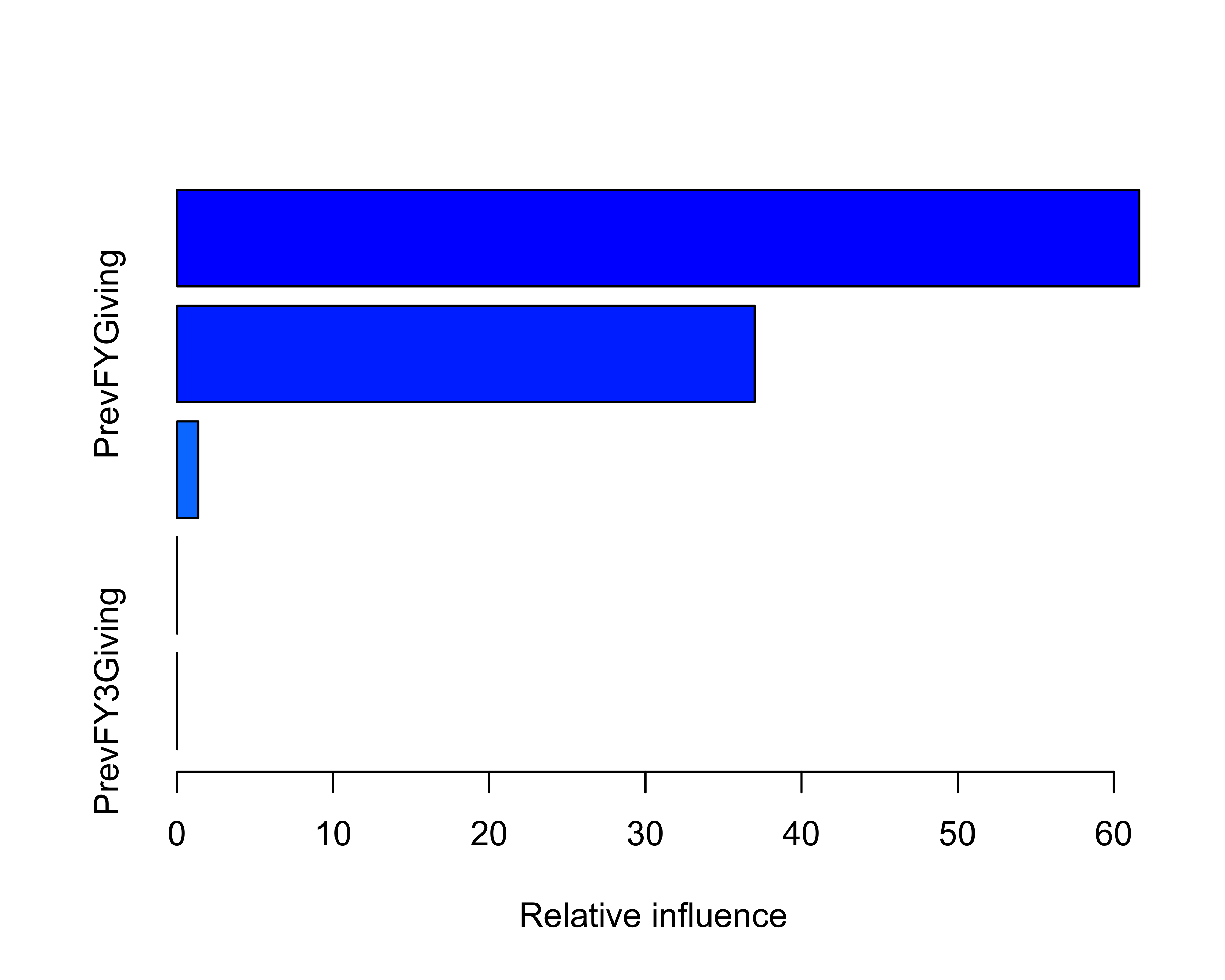
Let’s save the predictions.
donor_data$CurrFYGiving_pred_tdb <- predict.TDboost(
object = td1,
newdata = donor_data,
n.trees = 100)Are these predictions any better than the previous approaches? Let’s see by plotting.
ggplot(donor_data, aes(x = CurrFYGiving,
y = CurrFYGiving_pred_tdb)) +
geom_point() +
scale_x_sqrt(labels = dollar) +
scale_y_sqrt(labels = dollar) +
theme_bw() +
geom_smooth()
FIGURE 13.3: Actual versus prediction of current FY giving using TDBoost
You can see in Figure 13.3 that TDBoost severely underestimated the gift size, but there are many parameters that we didn’t change. Parameter tuning is an important task, which can yield better results. The RMSE without tuning was 15,849.
?TDboost into your R console window. Experiment with() various parameters and see whether you can obtain better results.
13.4 Neural Networks
As we saw in the previous chapter, NNs are an extension of generalized regression models. They work by creating a layer of nodes to minimize the error between the actual values and predictions. R comes with the nnet package.
Before you use the model, let’s go over the minimum number of parameters you need to provide.
size: How many nodes should there be in the hidden layer?linout: Is it a regression problem?maxit: How many times should the minimization (and adjustment of the parameters) occur?
Let’s build the model.
library(nnet)
nn <- nnet(CurrFYGiving ~ PrevFYGiving +
PrevFY1Giving + PrevFY2Giving +
PrevFY3Giving + PrevFY4Giving,
data = donor_data,
size = 8,
linout = TRUE,
maxit = 500)
#> # weights: 57
#> initial value 8670906034547.761719
#> iter 10 value 8669526260223.595703
#> final value 8669521216347.065430
#> convergedNow, let’s store those predictions.
donor_data$CurrFYGiving_pred_nn <- predict(nn)Let’s plot the predictions against the actuals. As you can see from Figure 13.4, this neural network did not do a good job at predicting the giving. The RMSE of this model was 15,850.
ggplot(donor_data, aes(x = CurrFYGiving,
y = CurrFYGiving_pred_nn)) +
geom_point() +
scale_x_sqrt(labels = dollar) +
scale_y_sqrt(labels = dollar) +
theme_bw() +
geom_smooth()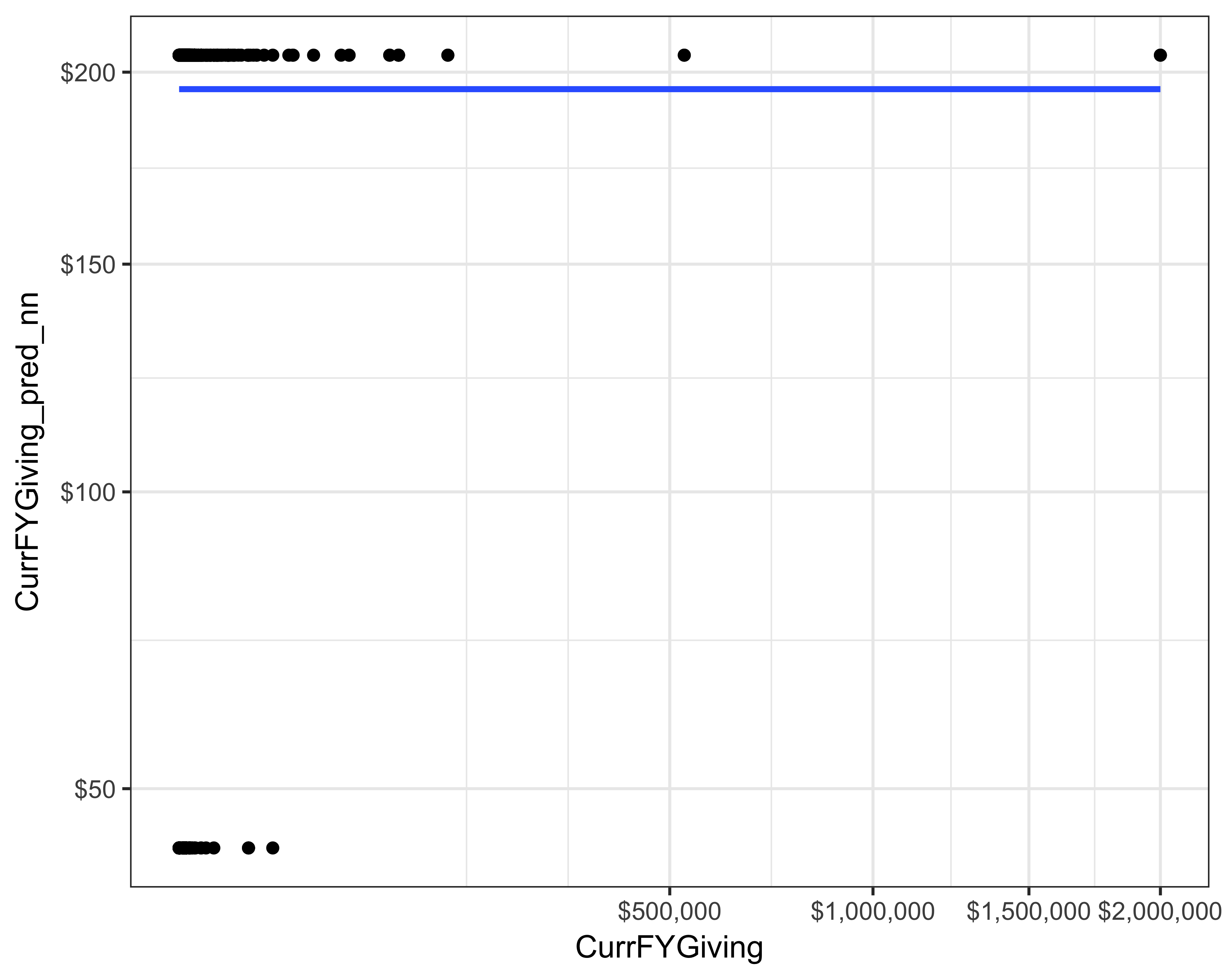
FIGURE 13.4: Actual versus prediction of current FY giving using neural networks
13.5 Method Evaluation
Building one model at a time is OK, but to evaluate models against each other, we need to find a better way of building and evaluating multiple models. Fortunately, there is a way. Bischl et al. (2016) built the mlr package to do exactly this.
Let’s take this step by step.
First, we need to make a list of “learners” or techniques we’re interested in applying. You can view all the available learners on mlr’s website.
If you select the techniques that come with R’s installation; you don’t need to install additional libraries. For example, the following code won’t return any errors.
library(mlr)
#> Warning: replacing previous import
#> 'BBmisc::isFALSE' by 'backports::isFALSE' when
#> loading 'mlr'
reg_learners <- list(makeLearner("regr.glm"),
makeLearner("regr.lm"))But if I want to add a random forest that’s part of the ranger package, I will get an error. I will need to install the ranger package before I add a learner. If you get an error, make sure that you have installed that package.
#Don't run
reg_learners <- list(makeLearner("regr.glm"),
makeLearner("regr.lm"),
makeLearner("regr.ranger"))Let’s select a few different learners.
library(mlr)
reg_learners <- list(makeLearner("regr.glm"),
makeLearner("regr.lm"),
makeLearner("regr.randomForest"),
makeLearner("regr.xgboost"),
makeLearner("regr.earth"))Next, how do you want to evaluate the models? Typically, we divide the data into training and test data sets, or we create cross-validation folds as seen earlier.
Let’s use a test (also known as “holdout”) set.
resample_plan <- makeResampleDesc("Holdout")
#you can also do a n-fold cross-validation
#resample_plan <- makeResampleDesc("CV", iters = 10) Next, mlr asks us to create a “task” that tells mlr how to build these models. We will use the same variables we have been using so far.
curr_fy_reg_task <- makeRegrTask(
id = 'donor_data',
data = select(donor_data,
starts_with("PrevFY"),
"CurrFYGiving"),
target = "CurrFYGiving")
#> Warning in makeTask(type = type, data = data,
#> weights = weights, blocking = blocking, : Provided
#> data is not a pure data.frame but from class
#> tbl_df, hence it will be converted.Finally, we build the models using the benchmark function.
benchmark_results <- benchmark(learners = reg_learners,
tasks = curr_fy_reg_task,
resamplings = resample_plan)We can see the results using the getBMRPerformances function.
getBMRPerformances(benchmark_results)
#> $donor_data
#> $donor_data$regr.glm
#> iter mse
#> 1 1 1.01e+09
#>
#> $donor_data$regr.lm
#> iter mse
#> 1 1 1.01e+09
#>
#> $donor_data$regr.randomForest
#> iter mse
#> 1 1 52507430
#>
#> $donor_data$regr.xgboost
#> iter mse
#> 1 1 39058708
#>
#> $donor_data$regr.earth
#> iter mse
#> 1 1 5.02e+08We can convert this result into a data frame and we can get the aggregate accuracy measure, which is the mean squared error (MSE) in this case, by using as.df = TRUE.
benchmark_results_df <- getBMRAggrPerformances(benchmark_results,
as.df = TRUE)
benchmark_results_df$rmse <- sqrt(benchmark_results_df$mse.test.mean)Since we have a data frame to work with now, it is easy to plot the results, as seen in Figure 13.5.
library(ggplot2)
library(scales)
ggplot(benchmark_results_df,
aes(x = reorder(learner.id, -rmse),
y = rmse)) +
geom_point(shape = 21, size = 3) +
scale_y_continuous(labels = comma) +
coord_flip() +
theme_bw(base_size = 14) +
xlab("Learner") + ylab("RMSE") 
FIGURE 13.5: RMSE of many models
The mlr package also offers some plotting functionality. Figure 13.6 shows a “violin” plot, which I don’t understand fully nor use. Since the example we ran above didn’t have variance in the error, I created these plots using some other criteria. But you can create such a plot by running the following command.
library(ggplot2)
plotBMRBoxplots(benchmark_results,
measure = mse,
style = "violin") +
aes(color = learner.id) 
FIGURE 13.6: Violin plot to compare models using the mlr package
style = "violin" option, you get a box plot, as shown in Figure 13.7.

FIGURE 13.7: Box plot to compare models using the mlr package
Buy Till You Die (BTYD) package offers customer lifetime value (CLV) calculations as well as other predictions. Use the RFM sample data file and experiment with the BTYD package.
If you’re enjoying this book, consider sharing it with your network by running
source("http://arn.la/shareds4fr")in yourRconsole.— Ashutosh and Rodger
References
Malthouse, Edward C, and Robert C Blattberg. 2010. “Can We Predict Customer Lifetime Value?” In Perspectives on Promotion and Database Marketing: The Collected Works of Robert c Blattberg, 245–59. World Scientific.
Perlich, Claudia, Saharon Rosset, Richard D Lawrence, and Bianca Zadrozny. 2007. “High-Quantile Modeling for Customer Wallet Estimation and Other Applications.” In Proceedings of the 13th Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, 977–85. ACM.
Yang, Yi, Wei Qian, and Hui Zou. 2017. “Insurance Premium Prediction via Gradient Tree-Boosted Tweedie Compound Poisson Models.” Journal of Business & Economic Statistics. Taylor & Francis, 1–15.
Tweedie, MCK. 1984. “An Index Which Distinguishes Between Some Important Exponential Families.” In Statistics: Applications and New Directions: Proc. Indian Statistical Institute Golden Jubilee International Conference, 579:6o4.
Jørgensen, Bent, and Marta C Paes De Souza. 1994. “Fitting Tweedie’s Compound Poisson Model to Insurance Claims Data.” Scandinavian Actuarial Journal 1994 (1). Taylor & Francis: 69–93.
Koenker, Roger. 2005. Quantile Regression. 38. Cambridge university press.
Koenker, Roger. 2017. Quantreg: Quantile Regression. https://CRAN.R-project.org/package=quantreg.
Yang, Yi, Wei Qian, and Hui Zou. 2016. TDboost: A Boosted Tweedie Compound Poisson Model. https://CRAN.R-project.org/package=TDboost.
Bischl, Bernd, Michel Lang, Lars Kotthoff, Julia Schiffner, Jakob Richter, Erich Studerus, Giuseppe Casalicchio, and Zachary M. Jones. 2016. “mlr: Machine Learning in R.” Journal of Machine Learning Research 17 (170): 1–5. http://jmlr.org/papers/v17/15-066.html.